How to Implement Binary Search Using Iterative Method

October 22, 2022 Abraham Smith

One of the most fundamental algorithms in computer science is the binary search algorithm. You can implement binary search using two methods: the iterative method and the recursive method. While both methods have the same time complexity, the iterative method is much more efficient in terms of space complexity.

The iterative process has a space complexity of O(1) compared to O(log) created using the recursive method. So how can you implement the binary search algorithm using the iterative method in C, C++ and Python?

What is binary search?

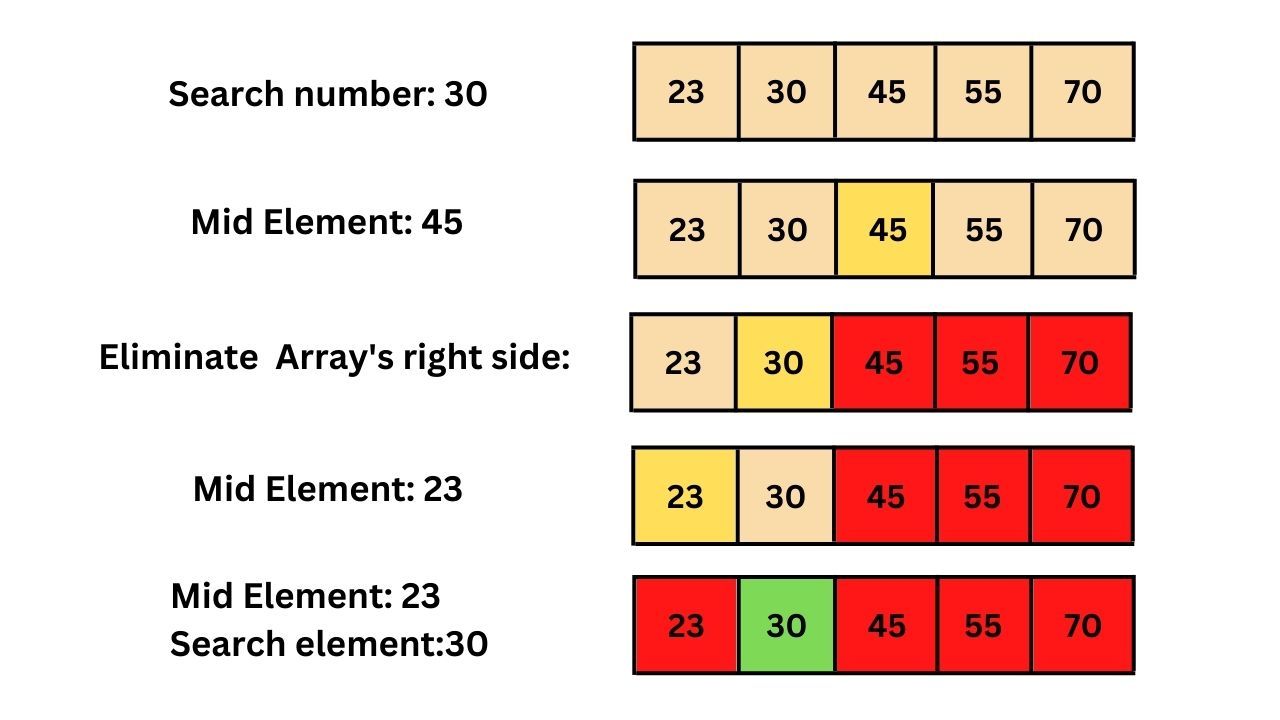
Binary search, also known as half-interval search, logarithmic search, or binary hashing, is an algorithm that finds and returns the position of an element in a sorted array. The search item is compared to the middle item. If you average the lower and upper bounds, you can find the middle elements.

If the search item is larger than the middle item, it means all the items on the left are smaller than the search item. So the control moves to the right side of the array (if the array is in ascending order) by increasing the lower bound to the next position of the middle element.

Similarly, if the search item is smaller than the middle item, it means that all items to the right are larger than the search item. So the control moves to the left part of the array by changing the upper bound to the previous position of the middle element.

This drastically reduces the number of comparisons compared to the linear search implementation, where the number of comparisons is equal to the number of elements in the worst case. This method is very useful for finding numbers in a phone book or words in a dictionary.

Here is a schematic representation of the binary search algorithm:

Binary search with C

Follow these steps to implement binary search using C:

The entire source code of the binary search program using C, C++, Java and Python is available in this GitHub repository.

The program defines a function binary search()which returns either the index of the found value or -1 if not available:

#include <stdio.h>int binarySearch(int arr[], int arr_size, int search_number) {
}

The function works by narrowing down the search space iteratively. Since binary search works on sorted arrays, you can calculate the middle, which doesn’t make sense otherwise. You can either ask the user for a sorted array or use sorting algorithms like Bubble or Selection Sort.

That low and high Variables store the indices that represent the boundaries of the current search space. center stores the index in the middle:

    int low = 0, high = arr_size - 1, mid;

The most important while() Loop delimits the search space. If the value of the low index ever becomes larger than the high index, then the search space is exhausted, so the value cannot exist.

    while (low <= high) {
}return -1;

After updating the midpoint at the beginning of the loop, there are three possible outcomes:

If the midpoint value is what you are looking for, return that index.
If the midpoint value is greater than the value you are looking for, reduce the high.
If the midpoint is lower, increase the low.

        
mid = (low + (high - low)) / 2;if (arr[mid] == search_number)
return mid;
else if (arr[mid] > search_number)
high = mid - 1;
else
low = mid + 1;

Test the function with user input. Use scanf() to get input from the command line, including the array size, its contents, and a number to search for:

int main() {
int arr[100], i, arr_size, search_number;
printf("Enter number of elements: ");
scanf("%d", &arr_size);
printf("Please enter numbers: ");for (i = 0; i < arr_size; i++) {
scanf("%d", &arr[i]);
}
printf("Enter number to be searched: ");
scanf("%d", &search_number);
i = binarySearch(arr, arr_size, search_number);
if (i==-1)
printf("Number not present");
else
printf("Number is present at position %d", i + 1);
return 0;
}

If you find the number, show its position or index, otherwise you won’t see a message that the number is there.

Binary search with C++

You can convert the C program to a C++ program by using the input-output stream and Use std namespace to avoid multiple repetition throughout the program.

#include <iostream>
using namespace std;

Use cout with extraction operator < Instead of printf() and cin with insertion operator >> Instead of scanf() and your C++ program is complete.

printf("Enter number of elements: ");
cout << "Enter number of elements: ";
scanf("%d", &arr_size);
cin >> arr_size;

Binary search with Python

Since Python doesn’t have built-in support for arrays, use lists. define function, binary search()which accepts three parameters, the list, its size and a number to search for:

def binarySearch(arr, arr_size, search_number):
low = 0
high = arr_size - 1
while low <= high:
mid = low + (high-low)
if arr[mid] == search_number:
return mid
elif arr[mid] > search_number:
high = mid - 1
else:
low = mid + 1
return -1

Initialize two variables, low and highto serve as the lower and upper bounds of the list. Similar to the C implementation, use a while Loop that delimits the search space. Initialize center to store the middle value of the list. Python provides the floor division operator (//), which returns the largest possible integer.

Perform the comparisons and narrow the search space until the mean equals the search number. If the search number does not exist, control returns -1.

arr_size = int(input("Enter number of elements: "))
arr=[]
print("Please enter numbers: ", end=" ")
for i in range(0,arr_size):
arr.append(int(input()))
search_number = int(input("Enter number to be searched: "))
result = binarySearch(arr, arr_size, search_number)
if result == -1:
print("Number not present")
else:
print("Number is present at position ", (result + 1))

Test the function with user input. Use Entry() to get the list size, its contents and a number to search for. Use int() to convert the string input Python accepts by default to an integer. To add numbers to the list, use the append () Function.

Phone call binary search() and pass the arguments. If you find the number, show its position or index, otherwise you won’t see a message that the number is there.

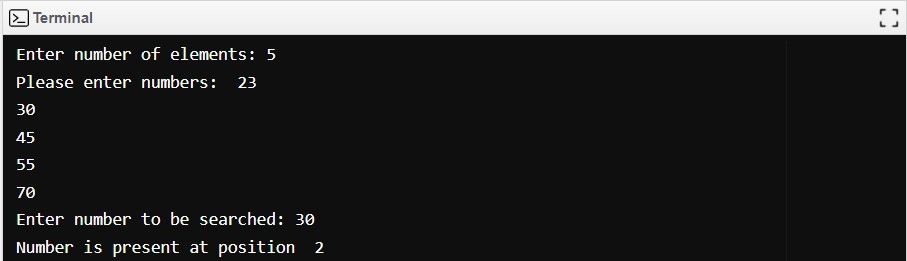
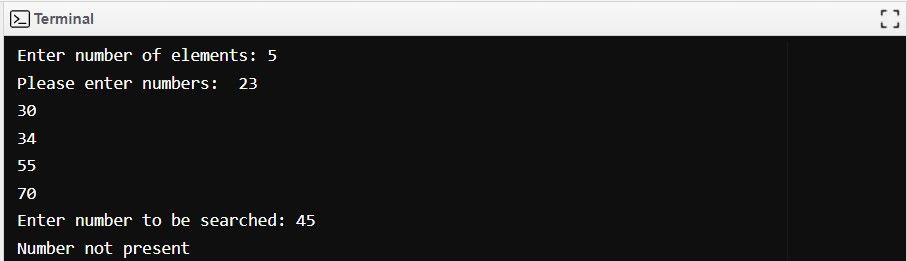
Binary search algorithm output

The following is the output of the binary search algorithm when the element is present in the array:

Binary search output when element is found

The following is the output of the binary search algorithm when the element is not present in the array:

Learn the basic data structures and algorithms

Search is one of the first algorithms you learn and is often asked in programming competitions, placements, and job interviews. Some other algorithms you should learn are sorting, hashing, dynamic programming, string matching, and primality testing algorithms.

In addition, it is important to understand the temporal and spatial complexity of algorithms. They are one of the most important concepts in computer science when determining the efficiency of an algorithm. With knowledge of data structures and algorithms, you will surely create the best programs.

unugtp